Subsampling and Averaging#

Due to the ordering of grid indices in global ICON grids, it is possible to quickly subsample and average datasets spatially.

[1]:

import intake

[2]:

import numpy as np
import xarray as xr
import yaml

[3]:

from gridlocator import merge_grid

getting some data#

We’ll first grab some datasets as usual. Here we use the prw variable from an ICON R02B09 run.

[4]:

col_url = "/pf/k/k202134/DYAMOND/Processing/full_catalog.json"
col = intake.open_esm_datastore(col_url)

[5]:

res = col.search(
    variable="prw",
    project="NextGEMS",
    model="ICON-SAP-5km",
    ensemble_member="dpp0052",
    operation="inst",
)

[6]:

d = res.to_dataset_dict(cdf_kwargs={"chunks": {"time": 1}})


--> The keys in the returned dictionary of datasets are constructed as follows:
        'project.institute.model.experiment.domain.frequency.grid.level_type.ensemble_member.operation'
100.00% [1/1 00:00<00:00]

We also need the grid information for plotting, so we’ll use a little helper function from gridlocator.py in this directory.

[7]:

ds = merge_grid(next(iter(d.values())))
ds

[7]:

<xarray.Dataset>
Dimensions:                         (time: 1969, cell: 20971520, nv: 3, vertex: 10485762, ne: 6, edge: 31457280, no: 4, nc: 2, max_stored_decompositions: 4, two_grf: 2, cell_grf: 14, max_chdom: 1, edge_grf: 24, vert_grf: 13)
Coordinates:
  * time                            (time) float64 2.02e+07 ... 2.02e+07
    clon                            (cell) float64 ...
    clat                            (cell) float64 ...
    vlon                            (vertex) float64 ...
    vlat                            (vertex) float64 ...
    elon                            (edge) float64 ...
    elat                            (edge) float64 ...
Dimensions without coordinates: cell, nv, vertex, ne, edge, no, nc, max_stored_decompositions, two_grf, cell_grf, max_chdom, edge_grf, vert_grf
Data variables: (12/92)
    prw                             (time, cell) float32 dask.array<chunksize=(1, 20971520), meta=np.ndarray>
    clon_vertices                   (cell, nv) float64 ...
    clat_vertices                   (cell, nv) float64 ...
    vlon_vertices                   (vertex, ne) float64 ...
    vlat_vertices                   (vertex, ne) float64 ...
    elon_vertices                   (edge, no) float64 ...
    ...                              ...
    edge_dual_normal_cartesian_x    (edge) float64 ...
    edge_dual_normal_cartesian_y    (edge) float64 ...
    edge_dual_normal_cartesian_z    (edge) float64 ...
    cell_circumcenter_cartesian_x   (cell) float64 ...
    cell_circumcenter_cartesian_y   (cell) float64 ...
    cell_circumcenter_cartesian_z   (cell) float64 ...
Attributes:
    references:              see MPIM/DWD publications
    title:                   ICON simulation
    CDI:                     Climate Data Interface version 1.8.3rc (http://m...
    history:                 /work/mh0287/k203123/GIT/icon-aes-dyw3/bin/icon ...
    source:                  git@gitlab.dkrz.de:icon/icon-aes.git@83f3dcef81e...
    institution:             Max Planck Institute for Meteorology/Deutscher W...
    Conventions:             CF-1.6
    intake_esm_varname:      ['prw']
    number_of_grid_used:     15
    grid_file_uri:           http://icon-downloads.mpimet.mpg.de/grids/public...
    uuidOfHGrid:             0f1e7d66-637e-11e8-913b-51232bb4d8f9
    intake_esm_dataset_key:  NextGEMS.MPIM-DWD-DKRZ.ICON-SAP-5km.Cycle1.atm.3...

Scatter-plotting with coarse resolution#

[8]:

%matplotlib inline
import matplotlib.pylab as plt

Plotting the entire globe in a small window can take very long for little benefit as there are many more grid cells than pixles available. Thus we need to combine sevaral grid cells into each pixel anyways. If we combine adjacent triangles before plotting, we still get a nice image at a fraction of the time. Please have a look at the chapter on grid index odering if you like to know more about why the following works. In short: every \(4^n\) adjacent grid cells are spatially close to each other, so we can combine those in a meaningful way.

In this example, we’ll look at two methods: averaging and subsampling. In the first case, we use reshape to convert the 1D data array into a 2D array where the 0-th axis will be the cell index at a coarser resolution and the 1-st axis will be the “details” within the coarse cell. We can use that representation to average (mean) across the details. The second case just selects every \(4^n\)-th element which happens to be the central cell of each coarse cell.

Let’s first arrange some variables and then do the plotting:

[9]:

coarsen = 4
a = ds.prw.isel(time=100).values
vmin = 0
vmax = a.max()

[10]:

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 7), dpi=300)
ax1.scatter(
    ds.clon[:: 4**coarsen],
    ds.clat[:: 4**coarsen],
    c=a.reshape(-1, 4**coarsen).mean(axis=-1),
    s=1,
)
ax2.scatter(
    ds.clon[:: 4**coarsen], ds.clat[:: 4**coarsen], c=a[:: 4**coarsen], s=1
)
ax1.set_title("var.reshape(-1, 4**n).mean(axis=-1)")
ax2.set_title("var[::4**n]")

for ax in (ax1, ax2):
    ax.axis("off")
    ax.set_xlim(-np.pi, np.pi)
    ax.set_ylim(-np.pi * 0.45, np.pi * 0.45)
../../_images/Processing_playing_with_triangles_subsampling_and_averaging_14_0.png

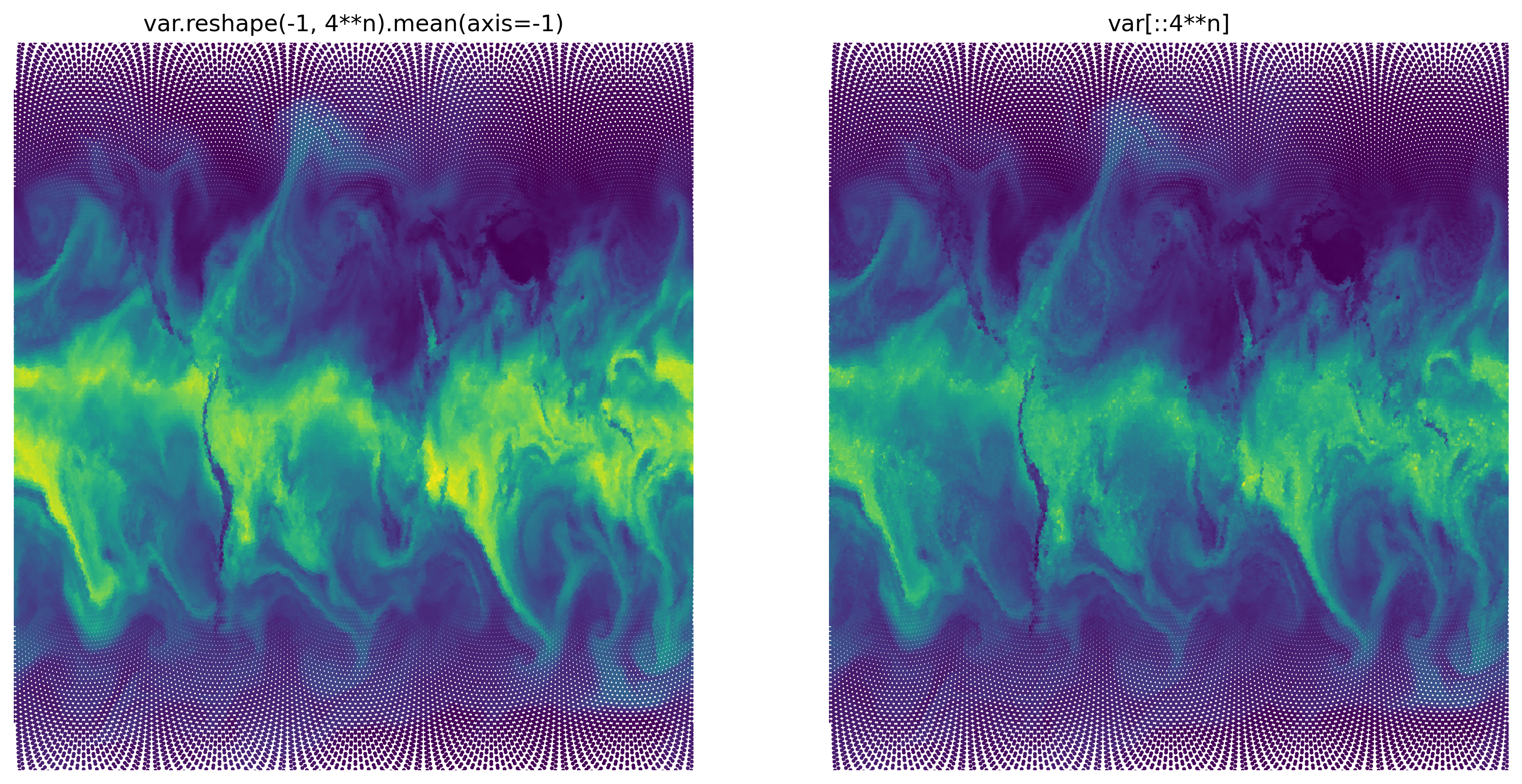
This works reasonably fast and creates a reasonable view of the globe. But it also creates a (quite nice) pattern of dots around the poles. This reminds us of the map projection which distorts the (roughly) equally spaced cell centers on the globe to an unequal spacing in 2d space. To create a slightly better version of the plot, we’ll look at another little trick:

scatter size trick#

If we increase the size of the scatter dot with latitude, the change in dot size roughly compensates for sample point spacing (this is of course dependent on the chosen projection). To illustrate this, we’ll use a larger scatter point size and coarsen our data even more.

[11]:

coarsen = 7

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 7), dpi=300)
ax1.scatter(
    ds.clon[:: 4**coarsen],
    ds.clat[:: 4**coarsen],
    c=a.reshape(-1, 4**coarsen).mean(axis=-1),
    s=10 / (np.cos(ds.clat[:: 4**coarsen] * 0.99) ** 2),
)
ax2.scatter(
    ds.clon[:: 4**coarsen],
    ds.clat[:: 4**coarsen],
    c=a.reshape(-1, 4**coarsen).mean(axis=-1),
    s=10 / (np.cos(ds.clat[:: 4**coarsen] * 0.99)),
)
ax1.set_title("1/cos**2")
ax2.set_title("1/cos")

for ax in (ax1, ax2):
    ax.axis("off")
    ax.set_xlim(-np.pi, np.pi)
    ax.set_ylim(-np.pi * 0.45, np.pi * 0.45)
../../_images/Processing_playing_with_triangles_subsampling_and_averaging_17_0.png

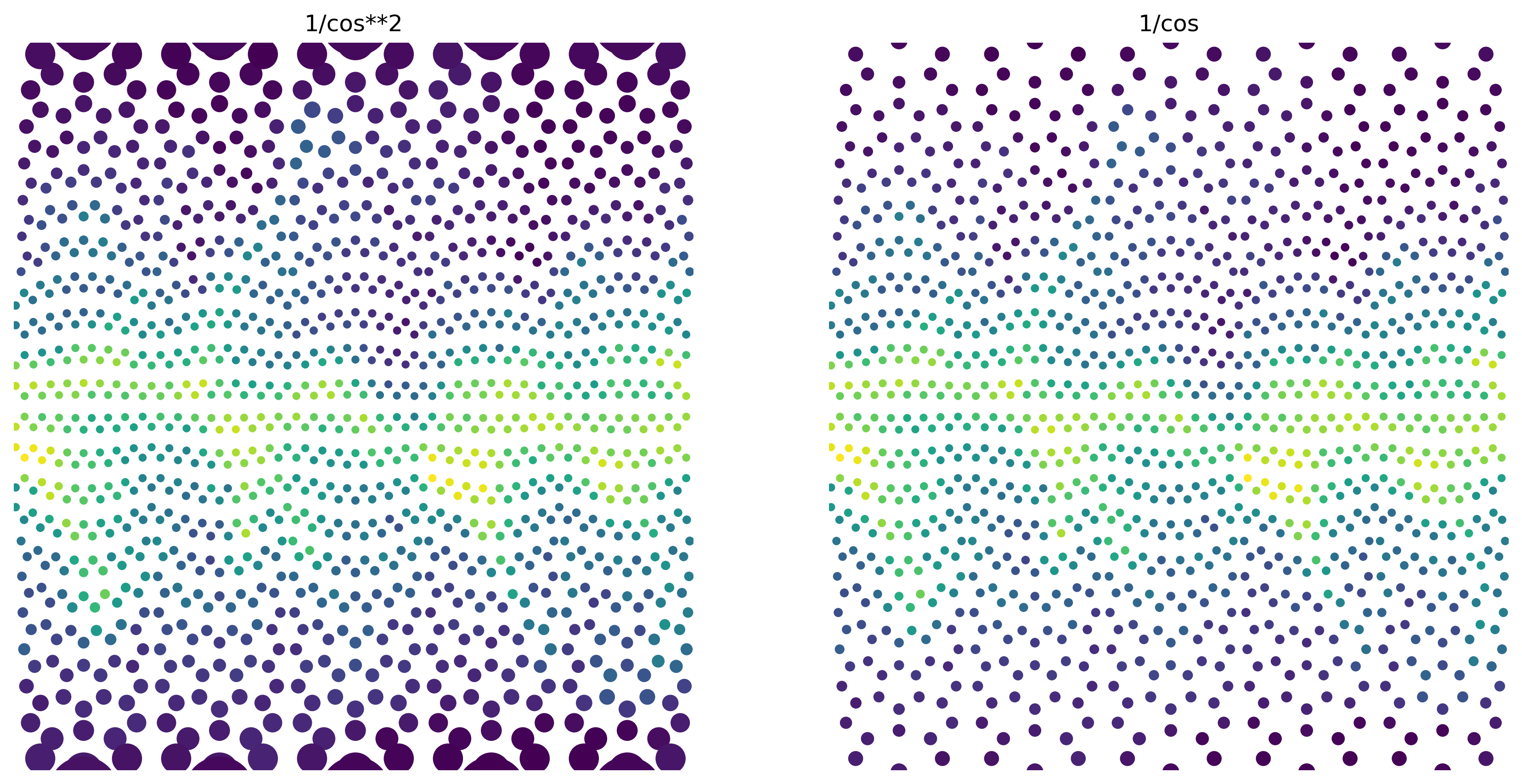
And now, the original plot:

[12]:

coarsen = 4

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 7), dpi=300)
ax1.scatter(
    ds.clon[:: 4**coarsen],
    ds.clat[:: 4**coarsen],
    c=a.reshape(-1, 4**coarsen).mean(axis=-1),
    s=1 / (np.cos(ds.clat[:: 4**coarsen] * 0.99) ** 2),
)
ax2.scatter(
    ds.clon[:: 4**coarsen],
    ds.clat[:: 4**coarsen],
    c=a[:: 4**coarsen],
    s=1 / (np.cos(ds.clat[:: 4**coarsen] * 0.99) ** 2),
)
ax1.set_title("var.reshape(-1, 4**n).mean(axis=-1)")
ax2.set_title("var[::4**n]")

for ax in (ax1, ax2):
    ax.axis("off")
    ax.set_xlim(-np.pi, np.pi)
    ax.set_ylim(-np.pi * 0.45, np.pi * 0.45)
../../_images/Processing_playing_with_triangles_subsampling_and_averaging_19_0.png

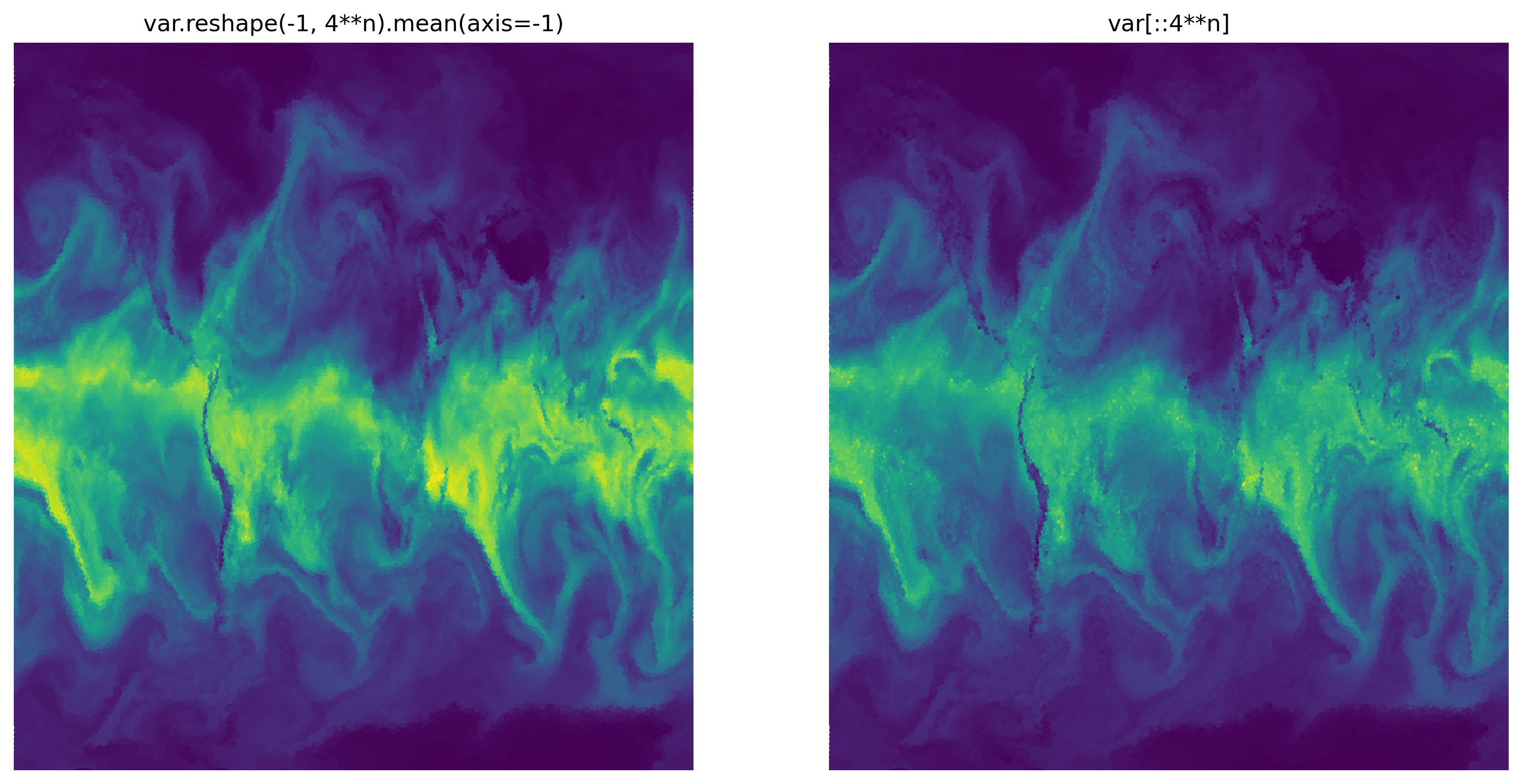
subregion#

Another option to reduce the amout of displayed data points is to select a subregion out of the whole domain. If we are interested in a box in latitude / longitude coordinates, the simplest thing to do would be to use a boolean expression as follows:

[13]:

mask = (
    (ds.clat.values > np.deg2rad(0))
    & (ds.clat.values < np.deg2rad(10))
    & (ds.clon.values > np.deg2rad(-60))
    & (ds.clon.values < np.deg2rad(-50))
)

Now, we’ll plot the subset of the data as above.

[14]:

plt.scatter(np.rad2deg(ds.clon[mask]), np.rad2deg(ds.clat[mask]), c=a[mask], s=1)

[14]:

<matplotlib.collections.PathCollection at 0x2b8e816c42e0>
../../_images/Processing_playing_with_triangles_subsampling_and_averaging_24_1.png